Combinación Lineal de Vectores

Decimos que un vector $\vec{v}$ es combinación lineal de otros ${\vec{a}}_{1}, {\vec{a}}_{2}, \dots {\vec{a}}_{n}$ cuando podemos expresarlo como operaciones de suma de los vectores ${\vec{a}}_{n}$ , cada uno de los cuales ha sido multiplicado por un escalar k_i :

$\vec{v} = k_{1} \cdot {\vec{a}}_{1} + k_{2} \cdot {\vec{a}}_{2} + \dots + k_{n} \cdot {\vec{a}}_{n}$

No te dejes abrumar, cuando trabajamos en el plano (2D), esto se simplifica enormemente.

El vector $\vec{v}$ es combinación lineal de los vectores ${\vec{a}}_{1}$ y ${\vec{a}}_{2}$ cuando puede expresarse según:

$\vec{v} = k_{1} \cdot {\vec{a}}_{1} + k_{2} \cdot {\vec{a}}_{2}$

Siendo k₁ y k₂ dos escalares (números) cualesquiera.

Ejemplos de combinación lineal de vectores

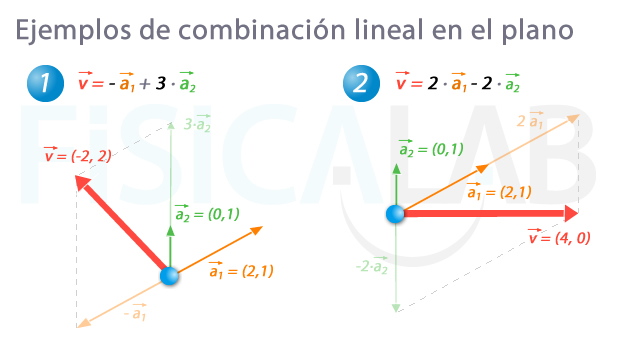
Algunos ejemplos

Los vectores rojos, en 1 y en 2, son combinación lineal de los vectores naranja y verde pues pueden obtenerse mediante sumas y restas de vectores proporcionales a estos últimos.

Decimos que un vector es linealmente dependiente de otro u otros cuando puede expresarse como combinación lineal de los demas. En el plano, dos vectores paralelos son linealmente dependientes. En caso contrario, son linealmente independientes.

¿Cómo expresar un vector en a partir de otros dos?

En el plano, cualquier vector puede ser expresado como combinación lineal de otros dos vectores no paralelos, es decir, como combinación lineal de otros dos vectores linealmente independientes.

Analíticamente

Basta aplicar la definición de combinación lineal estudiada, así, si queremos por ejemplo expresar el vector $\vec{v} = (- 2, 2)$ como combinación lineal de los vectores ${\vec{a}}_{1} = (2, 1)$ y ${\vec{a}}_{2} = (0, 1)$ , haríamos:

$\begin{matrix} \vec{v} = k_{1} \cdot {\vec{a}}_{1} + k_{2} \cdot {\vec{a}}_{2} \\ (- 2, 2) = k_{1} \cdot (2, 1) + k_{2} \cdot (0, 1) \end{matrix}$

Plantearíamos un sistema de ecuaciones igualando las componentes x por un lado, y las componentes y por otro, y resolveríamos:

$\begin{array}{r} - 2 = k_{1} \cdot 2 + k_{2} \cdot 0 \\ 2 = k_{1} \cdot 1 + k_{2} \cdot 1 \end{array}\} \Rightarrow \begin{array}{r} k_{1} = - 1 \\ 2 = k_{1} \cdot 1 + k_{2} \cdot 1 \end{array}\} \Rightarrow \begin{matrix} k_{1} = - 1 \\ k_{2} = 3 \end{matrix}$

Esto quiere decir que: $(- 2, 2) = - 1 \cdot (2, 1) + 3 \cdot (0, 1)$ .

Otro posible ejemplo sería expresar el vector $\vec{v} = (- 3, 1)$ como combinación lineal de los vectores ${\vec{a}}_{1} = (1, 1)$ y ${\vec{a}}_{2} = (- 1, 1)$ . En este caso:

$\begin{matrix} 3 = k_{1} - k_{2} \\ 1 = k_{1} + k_{2} \\ 4 = 2 k_{1} \end{matrix}\} \Rightarrow k_{1} = 2 \Rightarrow 1 = k_{1} + k_{2} \Rightarrow k_{2} = - 1$

Y por tanto $(3, 1) = 2 \cdot (1, 1) - (- 1, 1)$ .

Gráficamente

Centrémonos en este último ejemplo para explicar el proceso. Queremos expresar el $\vec{v}$ como combinación lineal de $\vec{a_{1}}$ y $\vec{a_{2}}$ , y se trata de buscar k1 y k2 gráficamente.

Cálculo gráfico de factores de vectores en combinación lineal

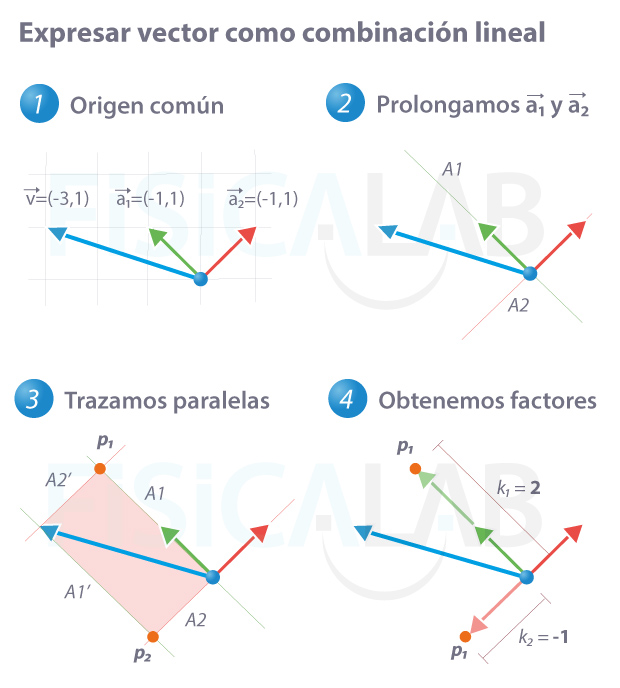
Método gráfico cálculo factores de combinación lineal

En primer lugar, tenemos que situar $\vec{a_{1}}$ , $\vec{a_{2}}$ , y $\vec{v}$ en un origen común. Posteriormente, prologamos las direcciones de los vectores aSUB1 y aSub2, obteniendo las rectas A1 y A2. En tercer lugar trazamos las paralelas de A1 y A2, que pasan por el extremo de $\vec{v}$ . Las llamaremos A1' y A2' respectivamente. Del corte de A1 con A2' obtenemos p1, que determinará k₁, y del corte de A2 con A1' obtenemos p2, que determinará k₂ como se ve en 4.

Estudiaremos el caso de vectores en el espacio tridimenional cuando veamos el concepto de base de un conjunto de vectores.

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.