Vector Unitario

Llamamos vector unitario a cualquier vector que tenga una unidad de longitud, o, dicho matemáticamente, todo aquel vector cuyo módulo valga 1.

$$\overrightarrow{a} \text{es unitario} \iff \left|\overrightarrow{a}\right|=1$$

Es también habitual expresar estos vectores mediante un "gorrito" encima de la letra que lleva su nombre, en lugar de una flechita, quedando, por ejemplo, $\hat{a}$.

Expresar cualquier vector a partir de su vector unitario

Podemos expresar cualquier vector $\overrightarrow{a}$ como el producto de su módulo por un vector unitario que tenga la misma dirección y sentido. A este vector unitario que lleva la información de dirección y sentido se le suele denotar con la letra u y el subíndice del vector original al que está asociado (en nuestro caso ${\overrightarrow{u}}_a$ ). Así, nos quedaría:

$$\overrightarrow{a}=\left|\overrightarrow{a}\right|·{\overrightarrow{u}}_a=a·{\overrightarrow{u}}_a$$

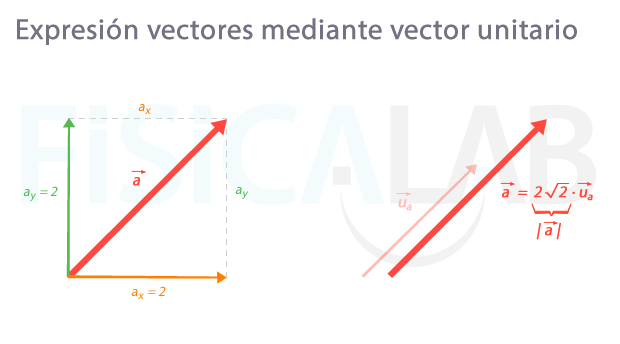
Expresión de un vector cualquiera mediante su vector unitario

El vector $\overrightarrow{a}=(2, 2)$ tiene por módulo $\left|\overrightarrow{a}\right|=\sqrt{2^2+2^2}=2·\sqrt{2}$. Cuando expresamos un vector cualquiera a partir de su vector unitario, toda la información de dirección y sentido la proporciona aporta el vector unitario asociado. La información de tamaño la aporta el propio módulo.

Componentes del vector unitario de un vector

La expresión anterior proviene de haber despejado la ecuación $\overrightarrow{a}=a·{\overrightarrow{u}}_a$. Nos dice simplemente que a partir de las componentes de un vector cualquiera $\overrightarrow{a}$, podemos calcular las componentes de su vector unitario asociado.

Ejemplo

Calcularemos las componentes del vector ${\overrightarrow{u}}_a$, unitario y con la misma dirección y sentido que el vector $\overrightarrow{a}=(2, 2)$ de la gráfica anterior.

$$\begin{array}{c}{\overrightarrow{u}}_a=\frac{{\displaystyle 1}}{\left|\overrightarrow{a}\right|}·\overrightarrow{a}=\frac{1}{\sqrt{2^2+2^2}}\left(2, 2\right)=\frac{{\displaystyle 1}}{{\displaystyle 2\sqrt{2}}}\left(2, 2\right)=\\ =\hspace{0.17em}\left(\frac{2}{2\sqrt{2}}, \frac{2}{2\sqrt{2}}\right)=\left(\frac{{\displaystyle 1}}{\sqrt{2}},\frac{{\displaystyle 1}}{\sqrt{2}}\right)\end{array}$$

Vectores unitarios en el sentido de los ejes

Existen un conjunto de vectores unitarios muy utilizados en física y otras ciencias. Se trata de los "mundialmente conocidos" vectores unitarios en el sentido de los ejes cartesianos:

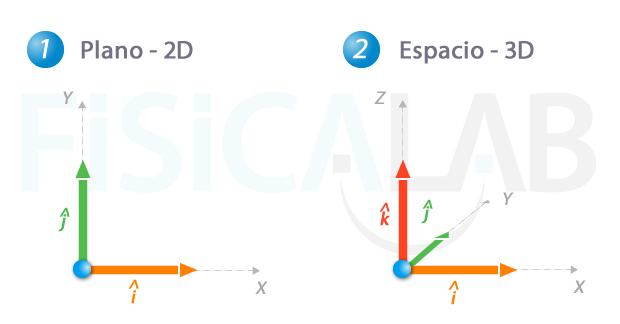
Vectores unitarios en el sentido de los ejes cartesianos

• $\hat{i}$, en el sentido positivo del eje x
• $\hat{j}$, en el sentido positivo del eje y
• $\hat{k}$, en el sentido positivo del eje z (en el caso de que estuviéramos en un espacio tridimensional en lugar de en un plano)

Estos vectores constituyen una base, concepto que estudiaremos en niveles posteriores. Por ahora, basta adelantar que es posible expresar cualquier vector como combinación lineal de ellos a partir de sus componentes. Por ejemplo:

$$\overrightarrow{v}=\left(3,-1\right)=3\hat{i}-\hat{j}$$

Conclusión

Los vectores unitarios nos permiten representar información de dirección y sentido, independientemente de la información relativa al módulo. Un vector unitario que represente un desplazamiento, y que apunte hacia el norte, por ejemplo, tiene módulo 1, pero no aporta ninguna información sobre la distancia específica que el cuerpo se ha desplazado hacia el norte. Simplemente indica "dirección norte". Esto es muy útil al hacer la resolución de problemas más sencilla en algunos casos, y es la base de los criterios de signos que estudiamos para algunas magnitudes vectoriales.