El Espejo Esférico

En óptica geométrica un espejo es cualquier superficie lisa y pulida capaz de reflejar los rayos de luz que llegan a él. El espejo refleja la luz haciendo que los rayos varíen su trayectoria y formando imágenes. En este apartado vamos a analizar como se ven las los objetos cuando estas superficies reflectoras son esféricas. Para ello veremos:

• Su ecuación fundamental y te mostraremos como puedes deducirla
• Qué ocurre con los focos y la distancias focales
• Qué ocurre con el aumento de las imágenes
• Cuáles son y cómo puedes dibujar sus gráficas
• Sus usos y  procesos de fabricación habituales

Para abordar los contenidos de este apartado cómodamente te recomendamos que antes comprendas bien el dioptrio esférico. ¿Preparado?

Ejemplo de espejos esféricos

Los espejos de seguridad situados en algunos comercios son un buen ejemplo del uso que se da a los espejos esféricos en nuestra sociedad. Cuando termines este apartado estarás en condiciones de entender por qué se forman las imágenes de esa manera tan particular.

Ecuación del espejo esférico

La ecuación fundamental del espejo esférico es una igualdad que relaciona la distancia al origen del objeto y la de la imagen con el radio de curvatura del espejo:

$$\frac{1}{s\text{'}}+\frac{1}{s}=\frac{2}{R}$$

Dónde:

• s , s' : Son las distancias del objeto y la imagen respectivamente al origen O, situado en el vértice óptico. Su unidad de medida en el Sistema Internacional (S.I.) es el metro ( m ). Según el criterio DIN de signos, que usamos, son negativas cuando están delante del espejo y positivos detrás

• R : Es el radio de curvatura del espejo esférico. Su unidad de medida en el S.I. es el metro ( m ). Según el criterio DIN:

  • Espejo convexo → R > 0.
  • Espejo cóncavo → R < 0.

Variables de la ecuación fundamental

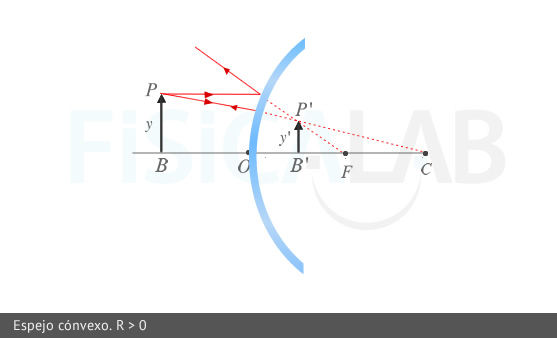
El rayo saliente del punto P se enfoca en el punto imagen P'. En la imagen se aprecian las variables de la ecuación fundamental, s, s' y R.

Recuerda que, además del criterio DIN, existen otros criterios de signos que puedes usar, pero ambos comparten la expresión anterior.

Comprobación

Podemos considerar la reflexión como un caso particular de refracción en el que n'=-n y usar la ecuación fundamental del dioptrio esférico. Así, nos queda:

$$\frac{n\text{'}}{s\text{'}}-\frac{n}{s}=\frac{n\text{'}-n}{R}\underset{n\text{'}=-n}{\Rightarrow }\frac{-n}{s\text{'}}-\frac{n}{s}=\frac{-n-n}{R}\Rightarrow \frac{\cancel{n}}{s\text{'}}+\frac{\cancel{n}}{s}=\frac{2·\cancel{n}}{R}\Rightarrow \frac{1}{s\text{'}}+\frac{1}{s}=\frac{2}{R}$$

Focos

En los dioptrios esféricos estudiábamos los focos objeto e imagen. El primero es el punto en el que hay que colocar el objeto para que los rayos salgan paralelos del dioptrio. El segundo es el punto en el que convergen los rayos provenientes de un objeto situado en el infinito, es decir, aquellos que llegan al dioptrio paralelos al eje óptico. En el caso del espejo, sólo existe un foco:

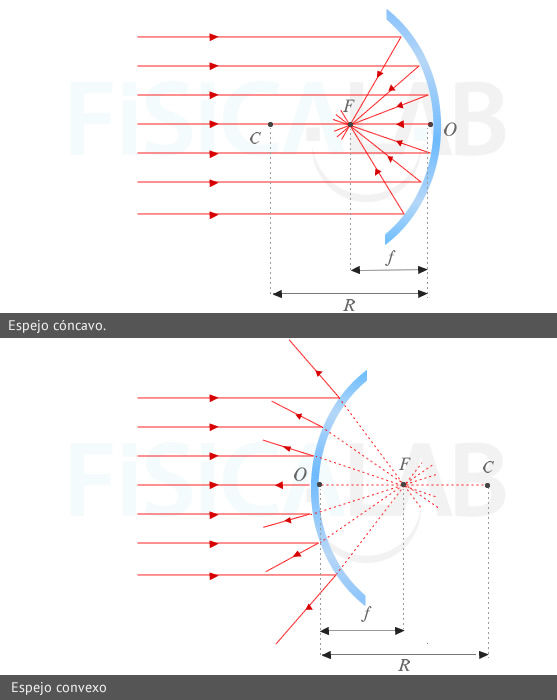
Focos en espejos esféricos

Tanto en los espejos cóncavos como en los convexos, la distancia focal es igual a la mitad del radio (f = R / 2). Los rayos que vienen del infinito pasan por el foco del espejo tras su reflexión.

Comprobación

Si partimos, esta vez, de las distancias focales a las que habíamos llegado en el caso del dioptrio esférico, y consideramos que, para el espejo esférico, n'=-n , podemos decir:

$$\left.\begin{array}{r}f=-R·\frac{n}{n\text{'}-n}\stackrel{n\text{'}=-n}{\overbrace{=}}-R\frac{n}{\left(-n\right)-n}=\frac{R}{2}\\ f\text{'}=R·\frac{n\text{'}}{n\text{'}-n}\stackrel{n\text{'}=-n}{\overbrace{=}}R·\frac{-n}{-n-n}=\frac{R}{2}\end{array}\right\}\Rightarrow f=f\text{'}=\frac{R}{2}$$

Aumento lateral

Tras su reflexión, los rayos forman imágenes de los objetos que pueden ser mayores, iguales, o menores que los objetos en sí.

Recuerda que se trata de una magnitud adimensional que te va a permitir determinar la altura de la imagen a partir de la del objeto original, o viceversa. Recuerda también que

• Si |A_L| > 1 , el tamaño de la imagen es mayor que el del objeto
• Si |A_L| < 1 , el tamaño de la imagen es menor que el del objeto
• Si A_L > 0 , la imagen es derecha
• Si A_L < 0 , la imagen está invertida

Comprobación

A partir de la expresión de aumento lateral en el dioptrio esférico, y asumiendo n'=-n , podemos hacer:

$$A_L=\frac{y\text{'}}{y}=\frac{n·s\text{'}}{n\text{'}·s}\stackrel{n\text{'}=-n}{\overbrace{=}}\frac{\cancel{n}·s\text{'}}{-\cancel{n}·s}=-\frac{s\text{'}}{s}$$

Gráficas

Es habitual obtener la posición y dimensiones de las imágenes de los objetos en el espejo desde un punto de vista gráfico. Para ello se usa lo que se conoce como diagrama de rayos. En ellos nos basta dibujar 2 rayos de trayectoria conocida, de los infinitos posibles. En realidad, es fácil dibujar al menos tres.

Observa que ya hemos visto a lo largo de este tema varios diagramas de rayos. Aquí tienes dos ejemplos más con los que ilustramos los rayos principales del espejo:

Rayos principales en espejos esféricos

La imagen superior representa un diagrama de rayos en el que un espejo cóncavo ( R < 0 ) forma una imagen del objeto real e invertida. La imagen inferior representa un diagrama de rayos en el que un espejo convexo ( R > 0 ) forma una imagen del objeto virtual y derecha.

Para dibujar un diagrama de rayos de un espejo esférico:

1. Comienza situando el eje óptico, el objeto y el espejo
2. Identifica el foco F (y opcionalmente el centro C)
3. Traza al menos 2 de los rayos principales de la punta P del objeto
4. El punto de intersección de los rayos es P', la imagen del punto P
5. Proyecta P' sobre el eje óptico para obtener la base de la imagen del objeto, B'

Experimenta y Aprende

Cargando...

Sistema óptico con espejo

Aquí puedes simular como se comporta un sistema óptico formado por un espejo. Pulsa sobre el botón play para comenzar a experimentar.

Construcción y usos

Una superficie metálica muy pulida es suficiente para fabricar un espejo. Es probable, sin embargo, que si observas con detenimiento algún espejo antiguo, descubras que se trata de una capa de vidrio y un recubrimiento de plata. Ese ha sido el método tradicional, aunque en la actualidad se puede utilizar un procedimiento de evaporación del aluminio en el vacío para conseguir un recubrimiento sobre una superficie altamente pulida.

La geometría de los espejos reales que se comportorten como los aquí descritos debe ser tal que permita a los rayos provenientes del infinito proyectarse en un sólo punto, el foco, se reflejen estos en el punto concreto del espejo donde se reflejen. La parábola es la figura geométrica que permite tal comportamiento, por lo que los espejos paraboloides se comportarían idealmente tal y como hemos descrito aquí.

La fabricación de espejos paraboloides perfectos no es sencilla, y por ello este tipo de espejos suelen ser caros. Sin embargo, dicha dificultad no la tenemos con los fabricados a partir de una esfera. La razón fundamental es sencilla: la pulimentación con una esfera es más sencilla que con un paraboloide, al permanecer en contacto todos los puntos mientras desplazamos una esfera sobre la otra. Esto no ocurre con el paraboloide. Sin embargo, los espejos así construidos presentan lo que se conoce como aberración esférica.

Aberración en espejos esféricos

La imagen superior representa un espejo paraboloide. Todos los rayos paralelos al eje se reflejan en el foco. En cambio, en la imagen inferior, observamos los efectos de la aberración esférica: los rayos se reflejan en distintos puntos según el lugar de la esfera en que se hayan reflejado.

Sin embargo, la aberración esférica no es un gran problema para nosotros, ya que trabajamos con rayos paraxiales, y todos ellos convergen, aproximadamente, en el mismo punto.

Zona paraxial en los espejos paraboloides y esféricos

En la zona paraxial, en verde, la esfera y el paraboloide son indistinguibles.

En relación a su utilización, los espejos esféricos están muy presentes en nuestra sociedad. Concretamente, respecto a los espejos cóncavos :

• Quizás estés familiarizado con espejos de maquillaje que agrandan la cara al ponerla cerca del espejo
• En los faros de los automóviles, estos espejos permiten que los rayos provenientes de la bombilla salgan paralelos
• En los telescopios reflectores se consigue hacer que los frentes de onda planos de la luz proveniente del espacio lejano converjan en un punto, formando una imagen nítida de los objetos lejanos

Por su parte, los espejos convexos :

• Suelen estar presentes en las salidas de garajes, por que permiten ampliar el campo de visión
• También se usan como espejos retrovisores en los automóviles