Triángulos Semejantes
En geometría, dos figuras son semejantes cuando su forma es la misma, sin importar su tamaño. Trasladando esta sencilla idea a los triángulos, podemos definir la semejanza entre triángulos.
Para conocer las matemáticas básicas que gobiernan el trabajo con figuras semejantes haremos uso de una de las más sencillas: el triángulo. En este apartado vamos a estudiar:
- Definición de semejanza de triángulos
- Criterios para identificar triángulos semejantes
- El perímetro de triángulos semejantes
- El área de triángulos semejantes
- El primer teorema de Tales, en el contexto de los triángulos
¿Preparado para convertirte en una auténtica "bestia" de las figuras semejantes?
Semejanza de triángulos
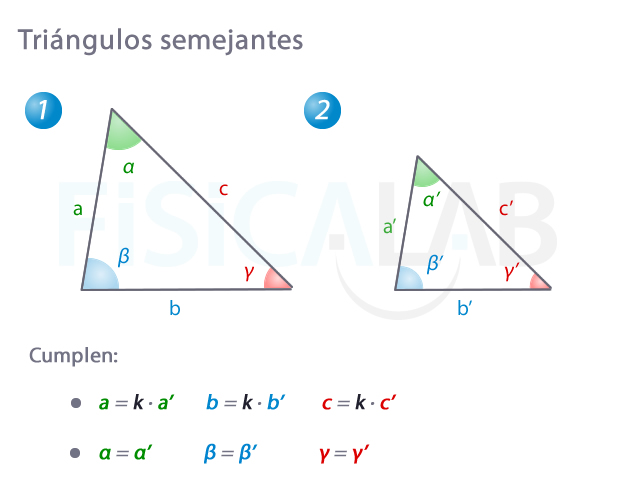
Decimos que dos triángulos son semejantes cuando tienen sus lados correspondientes proporcionales y sus ángulos correspondientes iguales.
Llamamos razón de semejanza k al valor por el que hay que multiplicar los lados de un triángulo para obtener su semejante. Es el cociente de lados homólogos. Así, en la figura anterior:
Criterios de semejanza
Para saber si dos triángulos son semejantes, basta comprobar una cualquiera de las siguientes afirmaciones:
- Tienen los tres lados proporcionales
- Tienen dos ángulos iguales (y por tanto el tercero, ya que entre los 3 siempre deben sumar 180º)
- Tienen dos lados proporcionales y el ángulo entre ellos igual
Triángulos rectángulos
Los criterios se simplifican cuando el triángulo es rectángulo (tiene un ángulo de 90º). Dos triángulos rectángulos son semejantes cuando podemos comprobar una cualquiera de las siguientes afirmaciones:
- Tienen los dos catetos proporcionales
- Tienen un cateto y la hipotenusa proporcionales
- Tiene un ángulo distinto del ángulo de 90º igual
Perímetro
El cociente de los perímetros de dos triángulos semejantes es igual a la razón de semejanza.
Comprobación
Efectivamente:
Área
El cociente de las áreas de dos triángulos semejantes es igual a la razón de semejanza al cuadrado.
Comprobación
En dos triángulos semejantes se cumple que la proporción entre las alturas h y h' también es la razón de semejanza, es decir:
De esta manera se cumple:
Primer teorema de Tales
Podemos enunciar el teorema de la siguiente manera.
El primer teorema de Tales establece que si trazamos una línea paralela a cualquier lado de un triángulo, el triángulo resultante será semejante al original.
A partir de esta sencilla afirmación, y de la existencia de una razón de semejanza en triángulos semejantes, existe una importante aplicación.
La proporción entre dos lados cualesquiera de un triángulo es la misma en los lados homólogos de todos sus triángulos semejantes.
Aclaramos esta idea con una imagen.
Como veremos en un apartado posterior, esta es la razón por la que en un triángulo rectángulo las razones de un ángulo no dependen del tamaño del mismo.
Existe otra forma de enunciar el primer teorema de Tales, relacionandolo con dos rectas cualesquiera, en lugar de con un triángulo. Volveremos a ello cuando estudiemos en detalle la geometría plana.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.