Tipos de ángulos
Enunciado
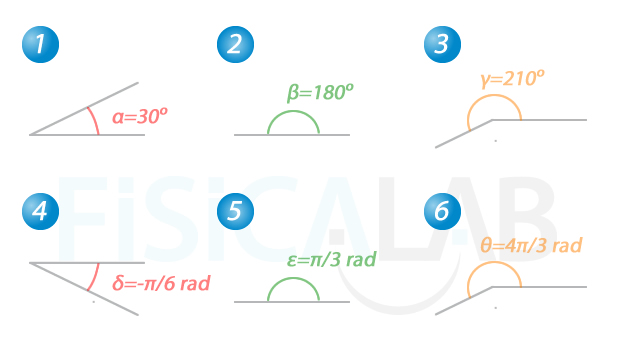
A partir de los siguientes ángulos...
- Determina el tipo de todos ellos, según las distintas clasificaciones propuestas
- A partir las rectas que delimitan el ángulo α, ¿qué ángulo concavo le correspondería?¿y para el ángulo ε?
- A partir las rectas que delimitan el ángulo γ, ¿qué ángulo convexo le correspondería?¿y para el ángulo θ?
- ¿Cómo son los ángulos α y ε según su suma?
- Sea ε'=2·ε, ¿cómo son los ángulos ε' y α según su suma?
- ¿Cómo son los ángulos α y δ según su suma?
- Dibuja α en una disposición en la que aparezca con otros 3 ángulos opuestos por el vértice, indicando la amplitud de cada uno de ellos
Solución
Consideraciones previas
Seguiremos las clasificaciones presentadas en el apartado sobre ángulos.
Resolución
1.-
Atendiendo a su amplitud, nos quedan:
- α, δ y ε son agudos, pues miden menos de 90º (o π/2 rad)
- β es llano, por medir 180º
Por otro lado, todos ellos, salvo el de 180º son oblícuos, pues sus amplitudes no son múltiplos de 90º.
2.-
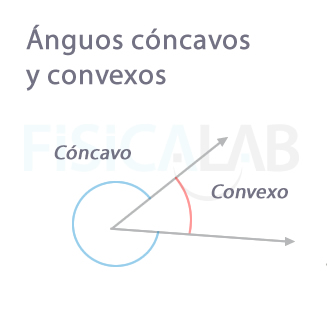
Recuerda que, dadas dos rectas, delimitan dos ángulos. Al de mayor amplitud lo denominamos cóncavo, y al de menor convexo.
Así pues, a partir las rectas que delimitan el ángulo α, el ángulo cóncavo que le correspondería sería aquel que, delimitado por las mismas rectas es de mayor amplitud, esto es, 360º-30º=330º.
Por otro lado, a partir las rectas que delimitan el ángulo ε, el ángulo cóncavo que le correspondería sería 2π-π/3=5π/3.
3.-
Según lo visto en el punto anterior, nos queda, al ángulo γ le correspondería un ángulo convexo de 360º-210º=150º.
Al ángulo θ le correspondería un ángulo convexo de 2π-4π/3=2π/3.
4.-
Puesto que π/3=60º, α+ε=90º, y por tanto son ángulos complementarios.
5.-
Puesto que ε'=2·ε=2·π/3=120º, α+ε'=180º, y por tanto son ángulos suplementarios.
6.-
Dado que δ=-π/6=-30º, se trata de ángulos opuestos o conjugados, pues suman 0º. Expresado δ en un ángulo del primer giro, equivaldría a -30º+360º=330º, que sumado a α resulta en 360º.
7.-
Prolongando las rectas que conforman α nos quedaría el ángulo α'=30º opuesto por el vértice a α, y â opuesto por el vértice a â'. Son 4 ángulos en total. Como â debe tener igual amplitud que â' nos quedan que â+â'=300º (300º=360º-α-α'), y por tanto â=â'=150º. Así pues:
No hemos encontrado ninguna fórmula destacable en este ejercicio.