Cálculo del Límite de una Función en el Infinito

El límite de una función f(x) cuando x tiende a infinito es el valor al que se aproxima la función a medida que la coordenada x crece indefinidamente. En la siguiente imagen queda recogido el concepto y la notación que se suele utilizar:

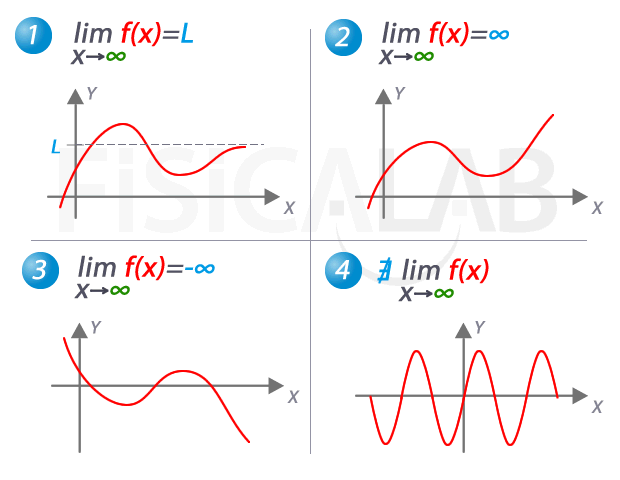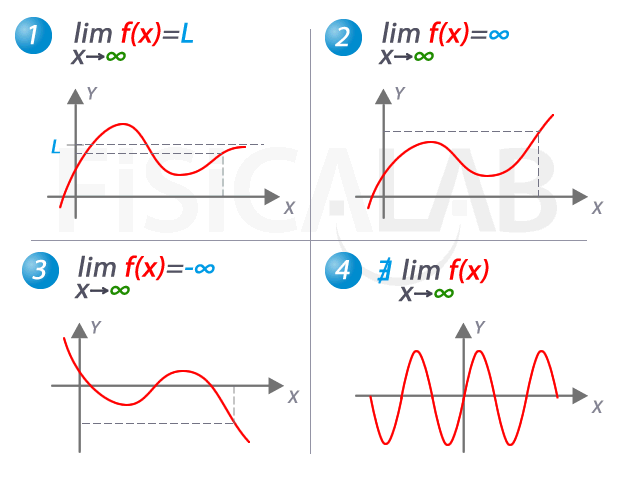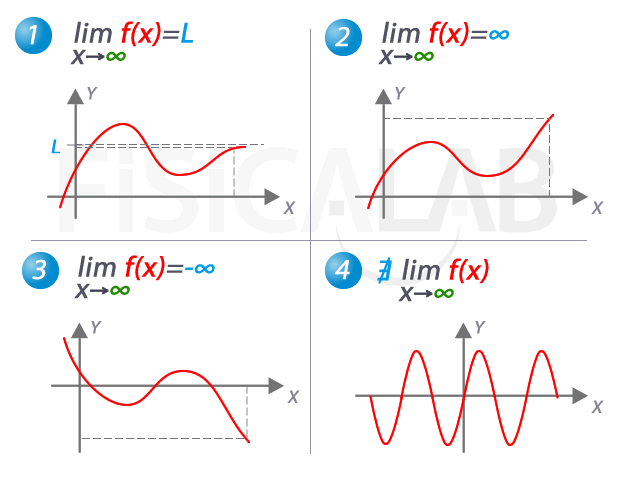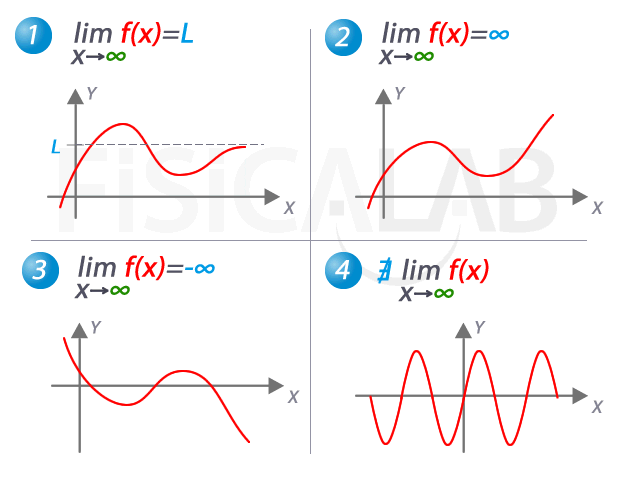
Notación y concepto

Los 4 posibles comportamientos de la función cuando el valor de x crece indefinidamente son los ilustrados en la figura. A nivel de notación $\underset{x\to \infty }{\lim }f\left(x\right)=L$, por ejemplo, se puede leer "f(x) tiende a L cuando x tiende a ∞", o bien "f(x)→L cuando x→∞

En este apartado vamos a darte las claves para el cálculo de ese límite, conocida la expresión de la función f(x). Lo haremos a través de numerosos ejemplos. Además, también vamos a considerar el caso de que x tienda a menos infinito, es decir, que la variable x crezca indefinidamente pero hacia la parte negativa del eje x.

• Método general
• Comparación de infinitos
  • Funciones de igual tipo
  • Funciones de distinto tipo
• Límite en infinito de polinomios
• Límite en infinito de raíces
• Límite en infinito del cociente de polinomios
• Propiedades

Si estás interesado en saber como calcular los límites de una función en un punto concreto, en lugar de en infinito, visita este apartado.

¿Empezamos?

Método general

Para resolver límites en el infinito seguimos los siguientes pasos:

1. Sustituimos x, en f(x), por ∞
2. Operamos con ∞
3. Si obtenemos un valor real concreto,∞ ó -∞, ya hemos terminado. Ese es el valor del límite buscado.
4. Si obtenemos una expresión indeterminada, debemos resolverla

El primer paso de la lista es bien sencillo. Se trata simplemente de poner ∞ allá donde ponga x en la función. Para operar con infinito, en el segundo paso, debes estar familiarizado con las expresiones que puedes obtener (por ejemplo 3/∞ , ∞-1000, etc.). Aunque te recomendamos que visites el apartado enlazado, te lo resumimos en la siguiente tabla. Ten presente que k representa un número real:

*Hemos prescindido de diferenciar los signos + y -. Este se determinará en cada caso según la relación entre el signo de k y el de ∞.

**En este caso hemos prescindido de diferenciar los signos +∞ y -∞ cuando el ∞ está en la base. En general, podrás operar antes de realizar la sustitución del límite para que el infinito elevado a la potencia sea positivo. Si no fuese así, recuerda que habrá que tener en cuenta la paridad del exponente, (-∞)^par=∞ y (-∞)^impar=-∞.

*** Estrictamente hablando, k/0 es una indeterminación que exige del cálculo de los límites laterales. No obstante, por convención, se suele decir que su valor es infinito, ya que el resultado de los límites laterales no puede ser otra cosa que infinito o menos infinito, indicándose, en cualquier caso, que la función diverge en el punto estudiado.

Como hemos dicho, si obtienes un valor concreto, ¡ya está!. Ese es el valor del límite. Pero tranquilo, si obtienes una indeterminación, no quiere decir que el límite no exista... solo que debemos resolverla, esto es, encontrar otro camino que haga desaparecer la indeterminación y nos dé el resultado del límite. Cada tipo de indeterminación tiene una manera concreta de resolverse, que estudiaremos en el apartado dedicado a ello.

Por el momento vamos a estudiar algunos casos sencillos para los que podemos prescindir de resolución de indeterminaciones. En todos ellos subyace la idea de la comparación de infinitos... veamos de qué se trata.

Comparación de infinitos

Ya sabemos que el infinito no es un valor concreto, sino más bien algo inmensamente grande a lo que nos acercamos. Cuando estudiamos valores de límites en el infinito estamos estudiando realmente el valor al que se acerca la función, es decir, su coordenada y. Imaginemos que la función se acerca (o tiende) a infinito. Cabe entonces hacerse la pregunta de si nos acercamos más rápido al infinito si nos "subimos" a un tipo de función o a otra. Y la respuesta es sí. Veámoslo con un ejemplo.

$$\begin{array}{cc}f\left(x\right)=x& g\left(x\right)=e^x\\ \underset{x\to \infty }{\lim }x=\infty & \underset{x\to \infty }{\lim }{e}^x=e^{\infty }=\infty \end{array}$$

Vemos que tanto la función f como g tienden a infinito. Sin embargo, observa:

$$\begin{array}{cc}f\left(100\right)=100& g\left(100\right)=e^{100}=2.68·{10}^{43}\\ f\left(10000\right)=10000& g\left(10000\right)=e^{10000}=7.22·{10}^{86}\\ f\left(1000000\right)=1000000& g\left(1000000\right)=e^{1000000}=1.94·{10}^{130}\end{array}$$

La función g(x) se aproxima al infinito mucho más rápidamente que la función f(x). Por cada dos ceros que gana f, g gana 43. Dicho de otra manera, por cada dos órdenes de magnitud en que aumenta f, g aumenta aproximadamente 43. Gráficamente:

Comparación de infinitos

No todas las funciones que tienden a infinito nos acercan a él a igual velocidad. Así, para valores suficientemente grandes, el crecimiento de la función exponencial, en rojo, es mucho más rápido que el de la función lineal, en azul.

De todo lo anterior cabe deducir que si "enfrentásemos" a f y g en una sola función, el infinito de g prevalecería sobre el de f. Por ejemplo:

$$\begin{gathered} \underset{x\to \infty }{\lim }\left(f\left(x\right)-g\left(x\right)\right)=\underset{x\to \infty }{\lim }\left(x-e^x\right)\underset{\infty -\infty \text{[IND]}\Rightarrow \\ \text{Por comp. de }\infty }{\underbrace{=}}-\infty \\ \underset{x\to \infty }{\lim }\left(g\left(x\right)-f\left(x\right)\right)=\underset{x\to \infty }{\lim }\left(e^x-x\right)\underset{\infty -\infty \text{[IND]}\Rightarrow \\ \text{Por comp. de }\infty }{\underbrace{=}}\infty \end{gathered}$$

Esta simple idea nos permitirá resolver algunas indeterminaciones de manera sencilla y directa. Pero antes de ir a ello, demos una definición más formal y algunas reglas para la comparación.

Funciones de igual tipo

Tú mismo puedes deducir que:

1. Si comparas potencias de x: Gana la de mayor exponente.

   Así, si comparamos por ejemplo x⁵ con 1000x², gana x⁵:

   $$\begin{gathered} \underset{x\to \infty }{\lim }\frac{x^5}{1000·x^2}=\underset{x\to \infty }{\lim }\frac{{\displaystyle 1}}{{\displaystyle 1000}}·x^3=\infty \\ \underset{x\to \infty }{\lim }\frac{{\displaystyle x^2}}{{\displaystyle 1000·x^5}}=\underset{x\to \infty }{\lim }\frac{{\displaystyle 1}}{{\displaystyle 1000·x^3}}=\frac{1}{\infty }=0 \end{gathered}$$

   Recuerda que los radicales también son potencias, \sqrt[n]{x^m}=x^{\frac{m}{n}}:

   $$\begin{gathered} \underset{x\to \infty }{\lim }\frac{\sqrt[6]{x^5}}{1000·x^2}=\underset{x\to \infty }{\lim }\frac{{\displaystyle 1}}{{\displaystyle 1000}}·\frac{{\displaystyle x^{\frac{{\displaystyle 5}}{6}}}}{x^2}=\underset{x\to \infty }{\lim }\frac{{\displaystyle 1}}{{\displaystyle 1000}}·\frac{{\displaystyle 1}}{x^{{\displaystyle \frac{7}{6}}}}=\frac{{\displaystyle 1}}{{\displaystyle \infty }}=0 \\ \underset{x\to \infty }{\lim }\frac{{\displaystyle \sqrt{x^5}}}{{\displaystyle 1000·x^2}}=\underset{x\to \infty }{\lim }\frac{{\displaystyle 1}}{{\displaystyle 1000}}·\frac{{\displaystyle x^{\frac{{\displaystyle 5}}{2}}}}{x^2}=\underset{x\to \infty }{\lim }\frac{{\displaystyle 1}}{{\displaystyle 1000}}·x^{\frac{1}{2}}=\infty \end{gathered}$$

   ... por lo que $\text{Grado}(1000·x^2)>\text{Grado}\left(\sqrt[6]{x^5}\right)$ pero $\text{Grado}(1000·x^2)<\text{Grado}\left(\sqrt{x^5}\right)$.

2. Si comparas polinomios: Gana el de mayor grado.

   Así, si comparamos por ejemplo x⁵-4x³ con 3x³+4x, ganaría x⁵-4x³:

   $$\begin{gathered} \underset{x\to \infty }{\lim }\frac{x^5-4x^3}{3x^3+2x}\underset{\frac{\left(\right)/x^3}{\left(\right)/x^3}}{=}\underset{x\to \infty }{\lim }\frac{{\displaystyle \frac{x^5}{x^3}}-{\displaystyle \frac{4x^3}{x^3}}}{{\displaystyle \frac{3x^3}{x^3}}+{\displaystyle \frac{2x}{x^3}}}=\underset{x\to \infty }{\lim }\frac{x^2-4}{3+{\displaystyle \frac{2}{x^2}}}=\frac{\infty -4}{3+0}=\infty \\ \underset{x\to \infty }{\lim }\frac{3x^3+2x}{x^5-4x^3}\underset{\frac{\left(\right)/x^3}{\left(\right)/x^3}}{=}\underset{x\to \infty }{\lim }\frac{{\displaystyle \frac{{\displaystyle 3x^3}}{{\displaystyle x^3}}+\frac{{\displaystyle 2x}}{{\displaystyle x^3}}}}{{\displaystyle \frac{x^5}{x^3}-\frac{4x^3}{x^3}}}=\underset{x\to \infty }{\lim }\frac{3+\frac{2}{x^2}}{x^2-4}=\frac{3+0}{\infty -4}=0 \end{gathered}$$

3. Si comparas funciones exponenciales de base mayor que 1: Gana la de mayor base.

   Así, comparando 3^x con 4^x, gana 4^x:

   $$\begin{gathered} \underset{x\to \infty }{\lim }\frac{4^x}{3^x}\underset{\frac{a^c}{b^c}={\left(\frac{a}{b}\right)}^c}{=}\underset{x\to \infty }{\lim }{\left(\frac{{\displaystyle 4}}{{\displaystyle 3}}\right)}^x=\infty \\ \underset{x\to \infty }{\lim }\frac{3^x}{4^x}\underset{\frac{a^c}{b^c}={\left(\frac{a}{b}\right)}^c}{=}\underset{x\to \infty }{\lim }{\left(\frac{{\displaystyle 3}}{{\displaystyle 4}}\right)}^x=0 \end{gathered}$$

4. Dos polinomios de igual grado o potencias de igual base (mayor que 1) son infinitos de igual orden.

   Así sucede comparando 6x⁵+2x con 3x⁵+x², y 4^x con 4^x+1:

   $$\begin{gathered} \underset{x\to \infty }{\lim }\frac{6x^5+2x}{3x^5+x^2}\underset{\frac{\left(\right)/x^5}{\left(\right)/x^5}}{=}\underset{x\to \infty }{\lim }\frac{{\displaystyle \frac{{\displaystyle 6x^5}}{x^5}+\frac{{\displaystyle 2x}}{x^5}}}{{\displaystyle \frac{{\displaystyle 3x^5}}{x^5}+\frac{{\displaystyle x^2}}{x^5}}}=\underset{x\to \infty }{\lim }\frac{{\displaystyle 6+\frac{{\displaystyle 2}}{x^4}}}{{\displaystyle 3+\frac{{\displaystyle 1}}{x^3}}}=2 \\ \underset{x\to \infty }{\lim }\frac{{\displaystyle 4^{x+1}}}{{\displaystyle 4^x}}=\underset{x\to \infty }{\lim }4·\frac{4^x}{4^x}\underset{\left[1\right]}{=}\underset{x\to \infty }{\lim }4·1=4 \end{gathered}$$

   Observa que, en [1], resolvemos 4^x/4^x=1, antes de sustituir las x por infinito. De lo contrario, nos encontraríamos con indeterminaciones innecesarias.

5. Si comparas funciones logarítmicas de igual o distinta base mayor que 1: los infinitos correspondientes son equivalentes a los de sus argumentos, independientemente de la base.

   Así, si comparamos por ejemplo ${\log }_3\left(x\right)$ con ${\log }_5\left(x\right)$, vemos que son de igual orden:

   $$\underset{x\to \infty }{\lim }\frac{{\log }_3\left(x\right)}{{\log }_5\left(x\right)}=\underset{x\to \infty }{\lim }\frac{{\displaystyle \frac{\ln \left(x\right)}{\ln \left(3\right)}}}{{\displaystyle \frac{\ln \left(x\right)}{\ln \left(5\right)}}}=\frac{\ln \left(5\right)}{\ln \left(2\right)}$$

Comparación de funciones de distinto tipo

Puedes llegar tú mismo a la misma conclusión observando la siguiente imagen:

Comparación de infinitos en funciones fundamentales

En la imagen 3 funciones tipo que se aproximan a infinito a medida que x se incrementa lo suficiente. En rojo la función exponencial, en azul una polinómica de grado uno (se trata de una recta), y en verde una logarítmica. Como ves, para valores suficientemente grandes, las funciones exponenciales siempre quedan por encima de las polinómicas, que a su vez quedan por encima de las lograrítmicas. Esto se debe a que el crecimiento de cada función se acelera de manera distinta.

Para entender el concepto de aceleración del crecimiento observa que, por cada unidad horizontal (distancia de un cuadro en horizontal), la función lineal siempre aumenta una unidad vertical. Diríamos que no se acelera su crecimiento en absoluto. Sin embargo, en la función exponencial esta distancia vertical aumenta cada vez más, para un mismo incremento de en el eje x. Diríamos que tiene una aceleración (positiva) de su crecimiento. Finalmente, en la logarítmica aumenta cada vez menos, con lo que tendría una aceleración negativa de su crecimiento.

Así pues, la exponencial nos aproximaría antes al infinito que la lineal, y si hiciéramos, por ejemplo: $\underset{x\to \infty }{\lim }\frac{x}{e^x}=0$.

Por otro lado, debes tener presente que:

Límites en infinito de polinomios

Cuando, siguiendo el método general señalado más arriba, sustituyes las apariciones de x por infinito en un polinomio, será habitual que te encuentres con indeterminaciones del tipo ∞-∞. Aún así, comparando los infinitos de los distintos integrantes del polinomio resulta claro que:

Por ejemplo:

• $$\begin{gathered} \underset{x\to \infty }{\lim }3x^2-x=[\infty -\infty ]\text{INDETERMINADA ;} \\ \text{Por comparación de }\infty \text{ , Orden }3x^2>\text{Orden }x\Rightarrow \underset{x\to \infty }{\lim }3x^2-x=\infty \end{gathered}$$

• $$\begin{gathered} \underset{x\to -\infty }{\lim }5x-x^3\underset{\underset{x\to -\infty }{\lim }f\left(x\right)=\underset{x\to \infty }{\lim }f\left(-x\right)}{=}\underset{x\to \infty }{\lim }5\left(-x\right)-{\left(-x\right)}^3=\underset{x\to \infty }{\lim }-5x+x^3=[-\infty +\infty ]\text{INDETERMINADA ;} \\ \text{Por comparación de }\infty \text{ , Orden }{x}^3>\text{Orden }5x\Rightarrow \underset{x\to \infty }{\lim }-5x+x^3=\infty \end{gathered}$$

Límites en infinito de raíces

Como hemos indicado, los radicales no son más que una forma de potencia, $\sqrt[n]{x^m}=x^{\frac{m}{n}}$. Por tanto, en algunos casos, podremos aplicar la misma regla. Por ejemplo:

• $$\underset{x\to \infty }{\lim }\sqrt{x^3-3x^2}=\infty$$

• $$\underset{x\to \infty }{\lim }\sqrt{3x^2-x^3}=\nexists$$

  ...porque el orden de x³ es el mayor, pero no podemos hacer la raiz de -∞, al ser raiz de algo negativo.

• $$\underset{\mathrm{x}\to \infty }{\lim }\sqrt{3{\mathrm{x}}^2+{\mathrm{x}}^3}-\sqrt[3]{2{\mathrm{x}}^5}=-\infty$$

  ...porque el orden de $\sqrt[3]{2x^5}$ (5/3) es mayor que el de $\sqrt{3x^2+x^3}$ (3/2).

Observa también con especial atención el siguiente caso:

$$\underset{x\to \infty }{\lim }\sqrt{3x^2-x}-\sqrt{5x^2+x}=-\infty$$

En este caso ambas raíces tienen igual grado (2/2=1), con lo que habría que prestar atención a los coeficientes, es decir, 3 y 5. Como el 5 es mayor, el infinito que prevalece es negativo.

Cocientes de polinomios

Por ejemplo:

• $$\underset{x\to \infty }{\lim }\frac{3x^2+2x^3}{5x-3x^2}=\left[\frac{\infty }{-\infty }\right]\text{Indeterminada. Por comp. de inf.}\Rightarrow \underset{x\to \infty }{\lim }\frac{{\displaystyle 3x^2+2x^3}}{{\displaystyle 5x-3x^2}}=\infty$$

  Porque grado P (3)>grado Q (2)

• $$\underset{x\to \infty }{\lim }\frac{3x^2+2x^3}{5x^4-x}=\left[\frac{\infty }{\infty }\right]\text{Indeterminada. Por comp. de inf.}\Rightarrow \underset{x\to \infty }{\lim }\frac{3x^2+2x^3}{5x^4-x}=0$$

  Porque grado P (3)<grado Q (4)

• $$\underset{x\to \infty }{\lim }\frac{2x-3x^2}{2x^2+3}=\left[\frac{-\infty }{\infty }\right]\text{Indeterminada. Por comp. de inf.}\Rightarrow \underset{x\to \infty }{\lim }\frac{2x-3x^2}{2x^2+3}=\frac{-3}{2}$$

  Porque grado P (2) = grado Q (2)

Pero también...

• $$\underset{x\to \infty }{\lim }\frac{\sqrt{x^3+2}}{x+5}=\left[\frac{\infty }{\infty }\right]\text{Indeterminada. Por comp. de inf.}\Rightarrow \underset{x\to \infty }{\lim }\frac{\sqrt[2]{x^3+2}}{x+5}=\infty$$

  Porque grado P (3/2)>grado Q (1)

• $$\underset{x\to \infty }{\lim }\frac{x+5}{\sqrt{x^5+3}}=\left[\frac{\infty }{\infty }\right]\text{Indeterminada. Por comp. de inf.}\Rightarrow \underset{x\to \infty }{\lim }\frac{x^1+5}{\sqrt[2]{x^5+3}}=0$$

  Porque grado P (1)>grado Q (5/2)

• $$\underset{x\to \infty }{\lim }\frac{\sqrt[3]{2x^5+3x}}{\sqrt[6]{4x^{10}-3x}}=\left[\frac{\infty }{\infty }\right]\text{Indeterminada. Por comp. de inf.}\Rightarrow \underset{x\to \infty }{\lim }\frac{\sqrt[3]{2x^5+3x}}{\sqrt[6]{4x^{10}-3x}}=\frac{\sqrt[3]{2}}{\sqrt[6]{4}}=\frac{2^{{\displaystyle \frac{1}{3}}}}{2^{{\displaystyle \frac{1}{3}}}}=1$$

  Porque grado P (5/3)= grado Q (10/6)

Propiedades del cálculo

Cuando operes con límites te será útil tener presente la siguiente tabla de propiedades. Sean $\underset{x\to \infty }{\lim }f\left(x\right)=a$ y $\underset{x\to \infty }{\lim }g\left(x\right)=b$. Entonces tenemos:

Visita el apartado enlazado para estudiar estas ideas y ver ejemplos con más detenimiento.